Skip to content

algorithm

科学刷题 灵茶山艾府

算法难度高，所以只有早上能够进入心流通道，其他时间不适合。

开发相关可以放到其他时间。

hot100

day1

哈希表-两数之和

参考题解：思路图解 programmercarl.com、代码实现 leetcode.cn

重点：Map，key 为数组值，value 为数组索引。

思路：

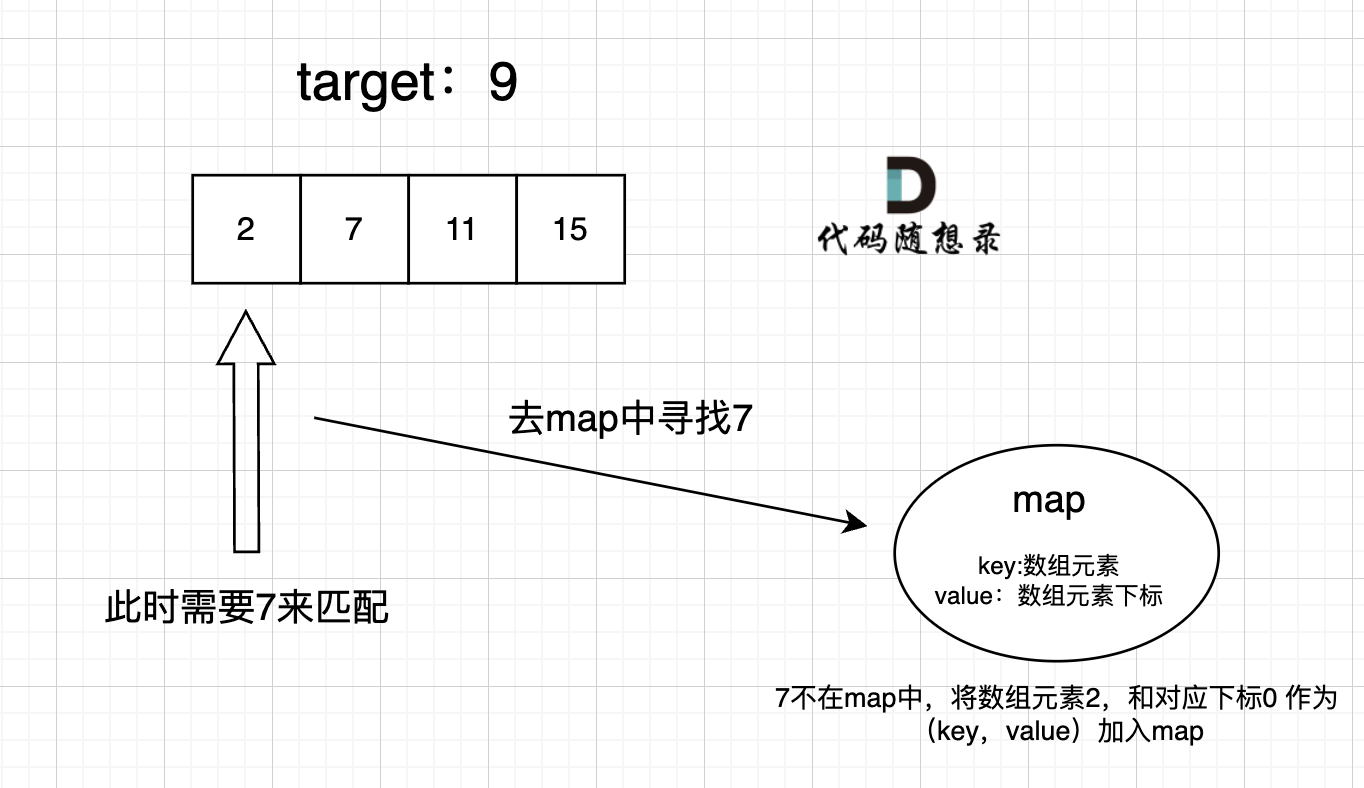
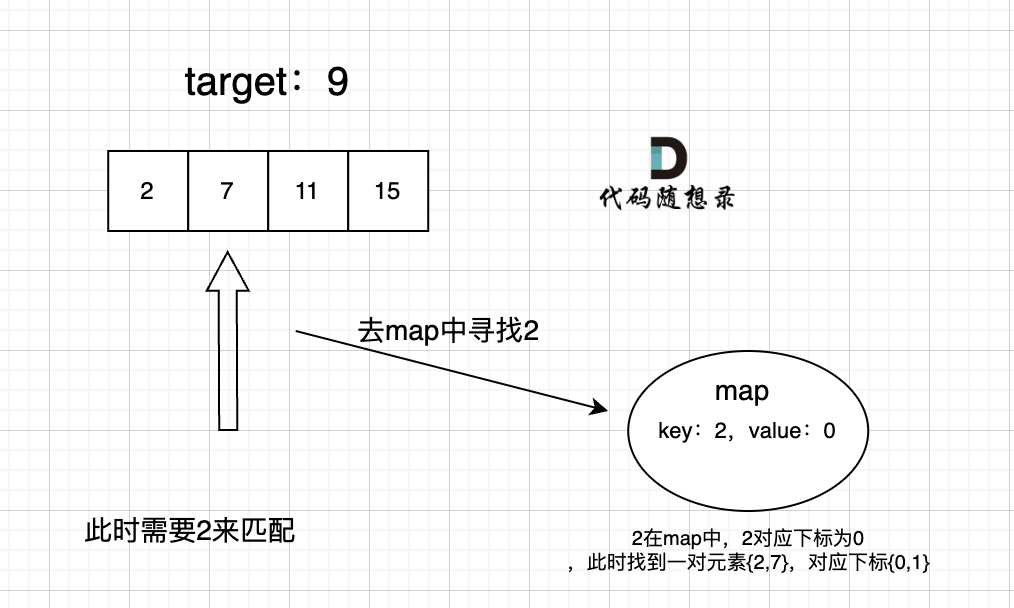
哈希表-字母异位词分组

参考题解 leetcode.cn

思路：排序，哈希表

代码：

代码里有很多不知道的用法。如 Map.getOrDefault 和 ArrayList<List<String>>(map.values())。

class Solution {
    public List<List<String>> groupAnagrams(String[] strs) {
        Map<String, List<String>> map = new HashMap<>();
        for (String str : strs) {
            // 排序
            char[] charArray = str.toCharArray();
            Arrays.sort(charArray);
            String sortedString = Arrays.toString(charArray);
            // 哈希表
            List<String> list = map.getOrDefault(sortedString, new ArrayList<String>());
            list.add(str);
            map.put(sortedString, list);
        }
        return new ArrayList<List<String>>(map.values());
    }
}

哈希表-最长连续序列

参考题解：代码实现 leetcode.cn

重点：

  • HashSet，既能去重，底层实现还内置了 HashMap，查询效率为 O(1)。

思路：

双指针-移动零

参考题解 leetcode.cn（图解清晰易懂）

思路：

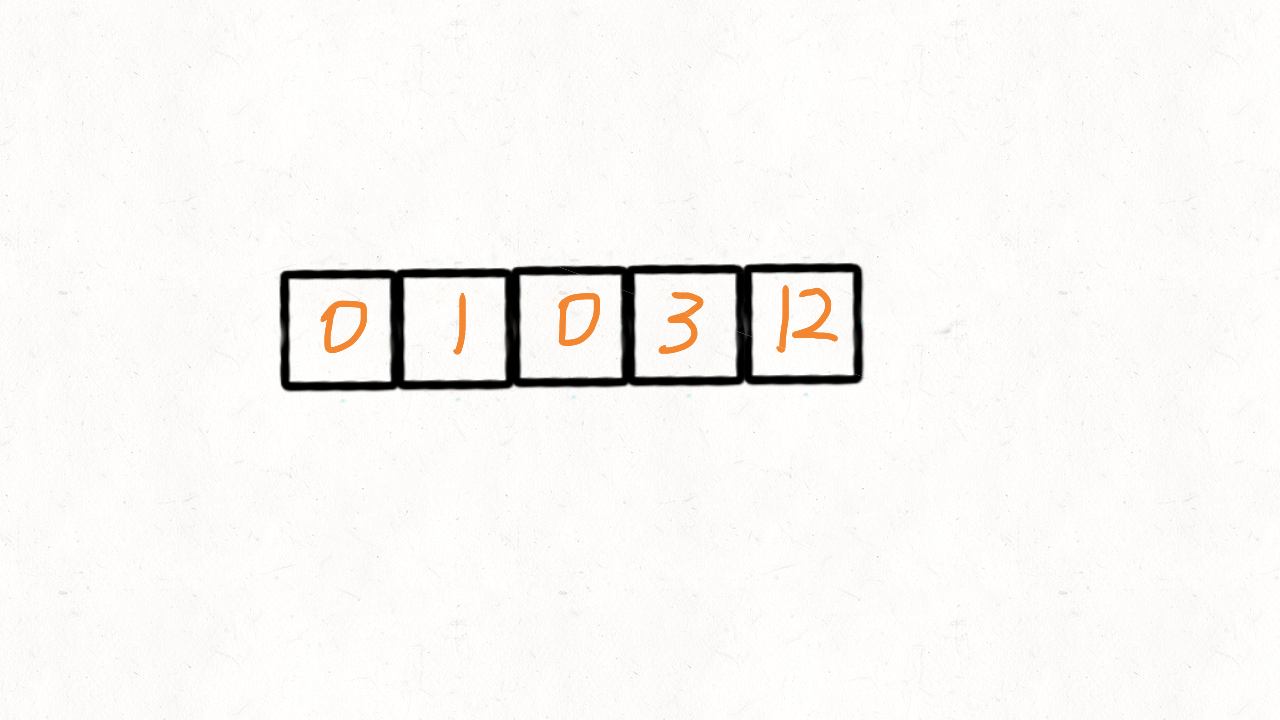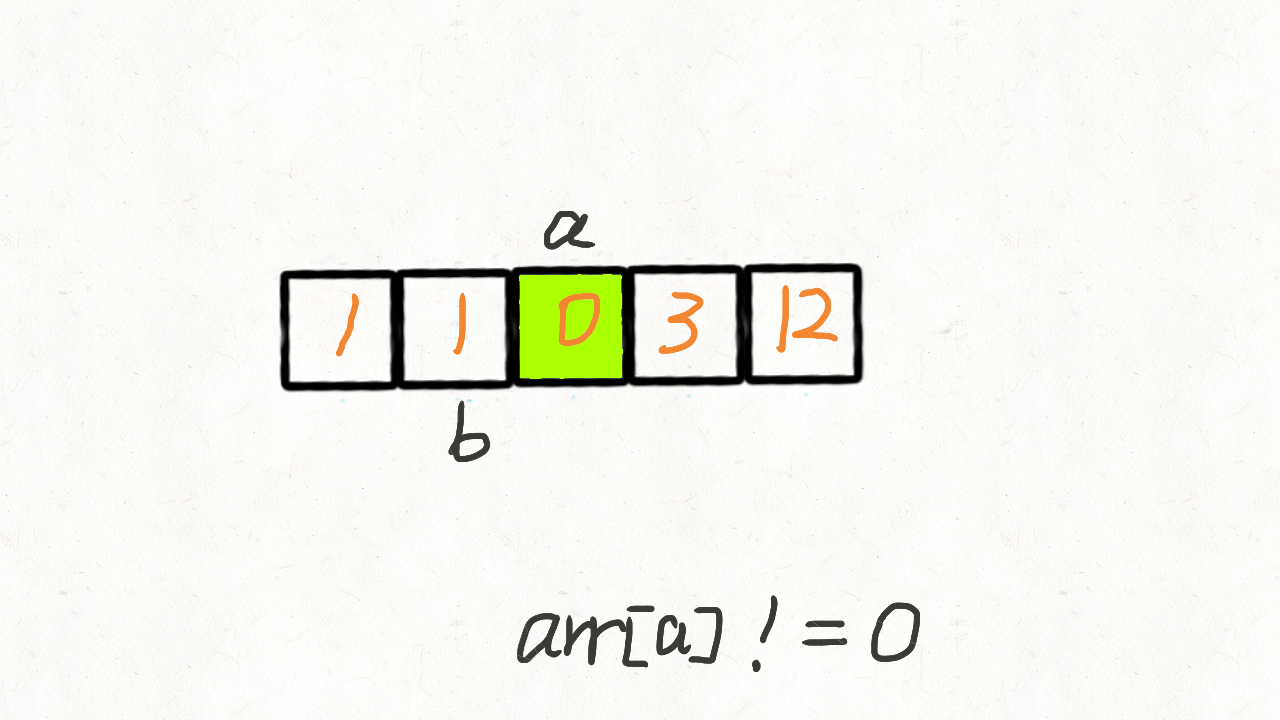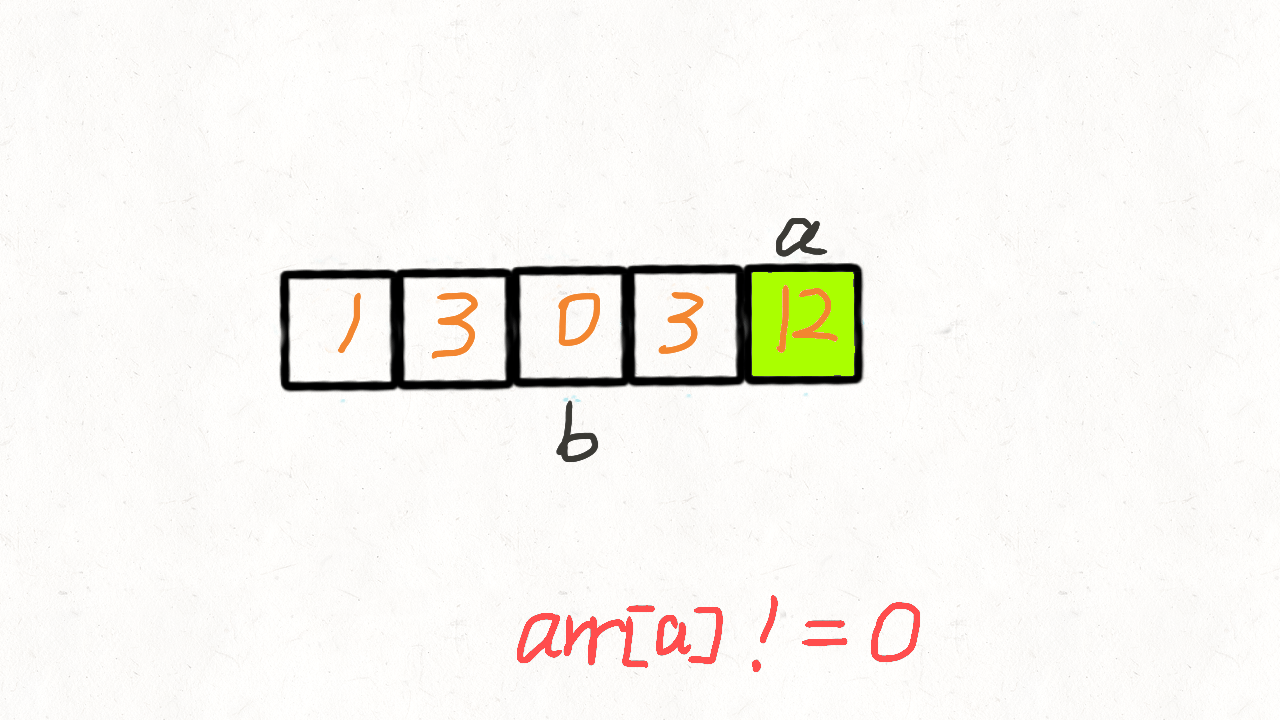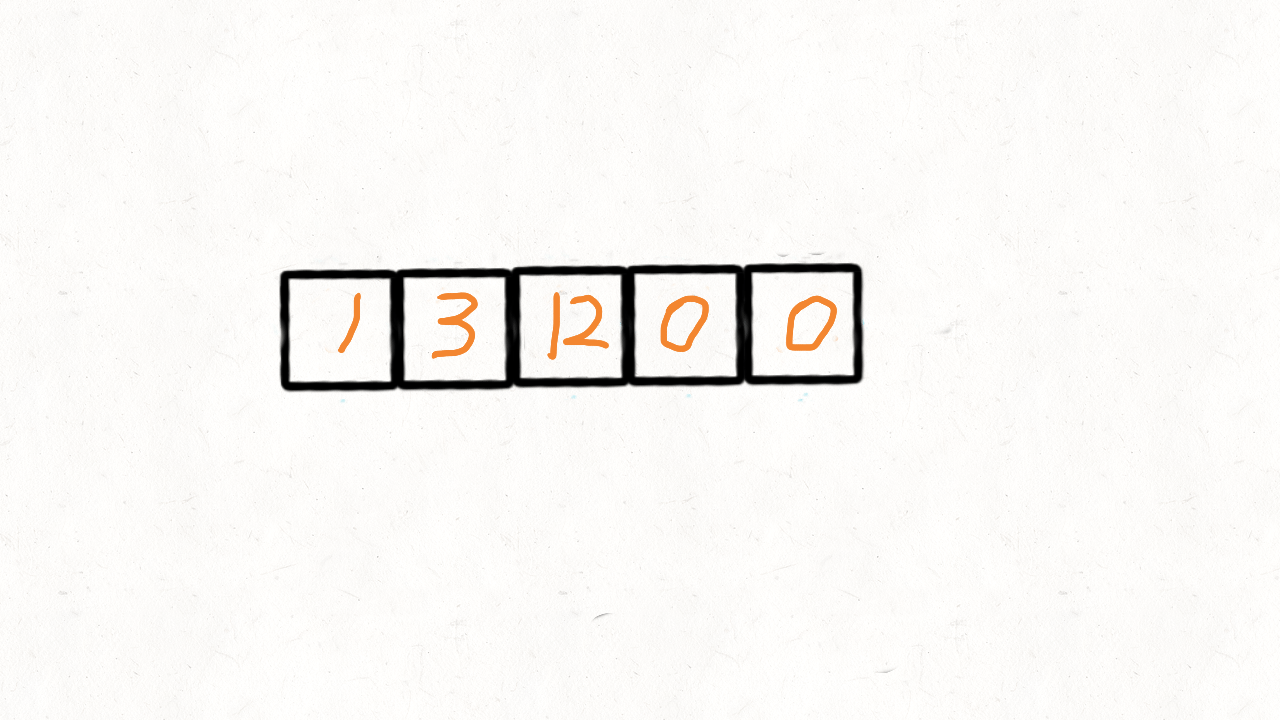
双指针-盛最多水的容器

参考题解：思路讲解 bilibili.com、优雅的代码实现 leetcode.cn

重点：

  • 左右指针相向移动，每次舍弃二者中更短的水槽版。
  • 面积公式：\(S(left, right) = Math.min(h[left], h[right]) * (right - left)\)

代码：

class Solution {
    public int maxArea(int[] height) {
        int i = 0, j = height.length - 1, res = 0;
        while(i < j) {
            res = height[i] < height[j] ? 
                Math.max(res, (j - i) * height[i++]): 
                Math.max(res, (j - i) * height[j--]); 
        }
        return res;
    }
}

day2

双指针-三数之和

暴力解法：

两层循环 + 两数之和思路

a + b + c == 0
for (a)
    for (b)
        if (map.containKey(0 - a - b))
// 难点在于 a b c 都要去重

正确思路：排序 + 三指针

重点：去重

  • 第一个元组的去重
  • left right 指针的去重

代码：题解 leetcode.cn（再结合自己 IDEA 中加的去重相关的注释）

理论基础-滑动窗口

思路：尺蠖运动（前后都要一步步来，不能跳）

模板

// 外层循环扩展右边界，内层循环扩展左边界
for (int l = 0, r = 0 ; r < n ; r++) {
    // 当前考虑的元素

    // 区间[left,right]不符合题意
    // （while 循环是重点，左指针慢慢移除元素挪到正确位置，而不是直接跳跃到正确位置）
    while (l <= r && check()) {
        // 扩展左边界
    }

    // 区间[left,right]符合题意，统计相关信息
}

不能用滑动窗口的场景：

数组元素不同号（要么全是正数，要么全是负数）。因为不同号的情况下滑动窗口会出现左指针向左移的情况，不好处理。

滑动窗口-无重复字符的最长子串

思路+代码 leetcode.cn（底下的第一条评论）

/**
 * 思路
 * 维护两个指针充当滑动窗口
 * 然后借助 HashMap 寻找判断右指针遍历到的元素是否重复
 * HashMap 的键是 s 中的字符，值是索引
 *
 * @param s
 * @return
 */
public int lengthOfLongestSubstring(String s) {
    int result = 0;
    Map<Character, Integer> map = new HashMap<>();
    for(int left = 0, right = 0; right < s.length(); right++) {
        // 如果当前字符已经在 map 中，且它的索引在左指针的左边
        while (map.containsKey(s.charAt(right))) {
            // 将左指针移动到重复字符的下一个位置
            map.remove(s.charAt(right));
            left++;
        }
        // 更新当前字符的位置
        map.put(s.charAt(right), right);
        // 计算当前子串的长度
        result = Math.max(result, right - left + 1);
    }
    return result;
}

滑动窗口-找到字符串中所有字母异位词

灵神给了两种方法，定长窗口和不定长窗口。

自己套模板的话是不定长窗口方法。

代码是让 AI 生成的，不太好理清思路，好好看看代码。

public List<Integer> findAnagrams(String s, String p) {
    List<Integer> ans = new ArrayList<>();
    // 用 HashMap 来统计 p 中每个字符的出现次数
    Map<Character, Integer> map = new HashMap<>();
    for (char c : p.toCharArray()) {
        map.put(c, map.getOrDefault(c, 0) + 1);
    }
    // 滑动窗口的左右指针
    int left = 0;
    // 记录当前窗口中字符的出现次数
    Map<Character, Integer> windowMap = new HashMap<>();
    for (int right = 0; right < s.length(); right++) {
        char c = s.charAt(right);
        // 右端点字母进入窗口
        windowMap.put(c, windowMap.getOrDefault(c, 0) + 1);
        // 如果窗口内的字符数量超过了 p 中字符的数量，收缩左边界
        while (windowMap.get(c) > map.getOrDefault(c, 0)) {
            char leftChar = s.charAt(left);
            windowMap.put(leftChar, windowMap.get(leftChar) - 1);
            left++;
        }
        // 如果当前窗口大小等于 p 的长度，且字符出现次数一致，表示是字母异位词
        if (right - left + 1 == p.length()) {
            ans.add(left);
        }
    }
    return ans;
}

子串-和为K的子数组

前缀和讲解 leetcode.cn

通过前缀和，我们可以把连续子数组的元素和转换成两个前缀和的差

题解 leetcode.cn

该题解中，从 前缀和方法 到 前缀和 + 哈希表方法 的讲解很不错。

代码

public int subarraySum(int[] nums, int k) {
    int result = 0;
    // 当前的前缀和
    int sum = 0;
    // key: 前缀和, value: 前缀和出现的次数
    Map<Integer, Integer> map = new HashMap<>();
    // 初始化前缀和为 0 出现的次数为 1，表示空子数组的情况
    map.put(0, 1);
    for (int i = 0; i < nums.length; i++) {
        // 更新当前的前缀和
        sum += nums[i];
        // 检查是否有一个之前的前缀和满足 sum - k
        if (map.containsKey(sum - k)) {
            // 将出现的次数加到结果中
            result += map.get(sum - k);
        }
        // 更新哈希表，记录当前前缀和出现的次数
        map.put(sum, map.getOrDefault(sum, 0) + 1);
    }
    return result;
}

day3

单调栈-每日温度

单调栈基础题。

单调栈-接雨水

关键：横着累计。

单调栈-柱状图的最大矩形

关键：如何求最大面积？

求出每一个高度对应的最大面积，然后比较出里面最大的。

已知高度，求最大面积，就是求最大的宽。

最大的宽 = 右边第一个比它小的索引 - 左边第一个比它小的索引 - 1。

因此，题就转换为了求每个高度左右第一个比他小的索引

所以使用单调栈。

总结-单调栈

单调栈分为单调递增和单调递减，分别适用于不同的场景。

  • 每日温度最基础，很好想。
  • 接雨水，栈单调递减。
  • 柱状图的最大矩形，栈单调递增。

典型场景：

image-20250222124946255

子串-滑动窗口最大值

思路 灵茶山艾府 bilibili.com

  • 坐飞机看山的例子，很形象

代码 代码随想录 programmercarl.com

day4

子串-最小覆盖子串

不行了，看不下去了，中午了，今天就四道题吧。

动态规划

完全背包

完全背包指每个物品都有无数个。

完全背包与01背包的不同：

  • 二维数组：递推公式
  • 一维数组：遍历顺序

重点：

二维数组解法 - 01背包与完全背包递推公式的区别：

首先，二者的递推关系都是：

最大价值 = Math.max(不放物品 i 的最大价值 + 放物品 i 的最大价值);

01背包每个物品只能添加一次，所以放物品 i 的情况不考虑本层物品，依赖于上一层左侧的值；

dp[j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);

完全背包每个物品能添加无数次，所以放物品 i 的情况需要考虑本层物品，依赖于本层左侧的值。

dp[j] = Math.max(dp[i - 1][j], dp[i][j - weight[i]] + value[i]);

一维数组解法 - 01背包与完全背包遍历顺序的区别：

由上面可知：01背包依赖于上层左侧，完全背包依赖于本层左侧；

所以一维数组解法中，内层遍历背包需要从小到大遍历。

518-零钱兑换II

纯完全背包：装满背包的最大价值

零钱兑换II：装满背包有多少种方法；装满背包的方法还是组合数，无顺序要求

与 494. 目标和 很类似，二者唯一区别是01背包与完全背包的区别。

重点：

  • 初始化
  • dp[0] = 1; 无明确推导逻辑，仅仅是从样例反推而来，题目描述不严谨。
  • 非零下标初始化为0，防止影响递推公式累加。
  • 遍历顺序：组合和排列
  • 纯完全背包两层 for 循环可上下颠倒
    • 物品 -> 背包（组合）
    • 背包 -> 物品（排列）

遍历顺序解释

（残存的思考。想不明白，举例子也想不明白，先记结论吧）

示例条件

  • 硬币面额：coins = [1, 2]
  • 总金额：amount = 3

物品 -> 背包（组合）

物品i\背包容量j 0 1 2 3
0 1 0 0 0
1 1 1{1} 1{11} 1{111}
2 1 1{1} 2{11 2} 2(dp[1][3]+dp[2][1]){111 12}

背包 -> 物品（排列）

物品i\背包容量j 0 1 2 3
0 1 0 0 0
1 1 1{1} 1{11} 1{111}
2 1 1{1} 2{11 2}

想了两个小时，根本想不明白 dp[2][3] 是怎么推导出来的，很多遍历中的边界条件，大脑思考谬误太多了，暂时放弃，先记忆结论吧。

复习

之前其实并没有做过标准的01背包与完全背包问题，中间四级考试间隔 20 天，此处知识忘记的太多了，所以借 标准01背包&完全背包-二维&一维数组 四个标准问题复习。

关键

  • 动规五部曲，先想好五步思路，再写代码：
    • 定义 dp 数组：几乎背会了。
    • 递归条件：看笔记。
    • 遍历顺序：边界条件其实很好写出来，能够想清楚整个过程，边界条件就很清晰了。
    • 初始化：
      • 问 AI，似乎背包与物品都从 0 开始遍历（即从背包容量为 0 与不装任何物品开始遍历）更加标准、好理解。
        • 这种思路更方便些，默认初始化为 0 即可。
      • 代码随想录讲的是：背包容量从 0 开始，物品从放第一个物品开始。
        • 这种做法算是第一种的优化，因为只放第一个物品的情况，可以很简单的手动遍历出来，复杂度更小，但是个人觉得这种情况下边界条件需要细心。
  • 一维数组相比二维数组，除了压缩状态，还将 “剩余背包容量是否能够容纳物品重量的判断” 整合进了遍历顺序当中，观感简洁，但是需要留心理解。

377-组合总和IV

花了6个小时，11:00-5:00，与自己和解了，二维数组-组合&排列本质依旧想不明白，放弃……

总结

494-目标和：01背包，固定物品，装满背包有多少种方法。

  • 笔记在平板上，先思考二维数组解法；
  • 然后根据二维数组状态压缩，推出一维数组解法；

518-零钱兑换II：完全背包，固定物品，组合，装满背包有多少种方法。

  • 二维数组正常思考能做出来；
  • 一维数组解法是根据 494-目标和 知道的。

377-组合总和IV：完全背包，固定物品，排列，装满背包有多少种方法。

  • 二维数组如何做出排列？根本理解不了，放弃；
  • 一维数组解法就是：把 518-零钱兑换II 一维数组解法的遍历顺序互换。

所以，这几道题的思考记忆关系就是：

494-目标和-二维数组 -> 494-目标和-一维数组 -> 518-零钱兑换II-一维数组 -> 377-组合总和IV-一维数组

做法

518-零钱兑换II 交换物品背包遍历顺序即可。

注意

注意初始化，将背包容量为 0 的情况初始化为 1。

进阶

进阶爬楼梯问题，一次可以爬 0~n，爬 m 阶台阶方法数。解法与本题同理，都是 动态规划-完全背包-排列 问题。

322-零钱兑换

难点

定义 dp 数组：装满容量为 j 的背包，最少物品为 dp[j]。

递推公式：dp[j] = Math.min(dp[j - coins[i]] + 1, dp[j]);。

本题的过程不难想象，先遍历物品，再遍历背包，遍历出只有第一个钱币情况的个数，然后逐个添加，再遍历，通过递推公式取最小值。（如果看不懂，想象一下过程就好了）

注意

初始化。之前的题大多是比较子问题谁更大，所以初始值为 0。这道题比较谁更小，所以初始值为 Integer.MAX_VALUE。

279-完全平方数

重点是问题的转换：给这些物品（完全平方数），装满容量为n的背包，求装满背包最少使用多少物品。

转换后这道题的思路就与上一题一摸一样了。

139-单词拆分

思路

有无限数量的物品（wordDict），判断是否能够装满背包。

代码随想录是按完全背包讲解的，但是自己思考了下感觉有些牵强，思路更像是双指针，只是代码写出来很像完全背包。

示例

s = "applepen"; wordDict = ["apple", "pen"];

i s.substring(j, i)（左闭右开） isAppear?
0 0~0 默认初始化 y
1 0~1 n
2 0~2 n
3 0~3 n
4 0~4 n
5 0~5 y
6 5~6 n
7 5~7 n
8 5~8 y

小重点

String.substring(int beginIndex, int endIndex) 方法，参数区间是左闭右开。

原因：

  1. 计算长度简单：length = endIndex - beginIndex。
  2. 分段方便：例如提取索引 0~4 和 4~8，endIndex 与下一个 beginIndex 连续，不会重复字符。

左闭右开的设计在编程中似乎很常见，例如 Python 的切片、C++ 的区间。

背包总结

代码随想录-动态规划-背包问题总结篇

198-打家劫舍

正常 DP，拆分为子问题，然后比较偷与不偷的金额大小，钱尽可能偷多。

注意

题目要求的是偷的房间不能相邻，没要求必须隔一个，也可以隔多个。

213-打家劫舍II

在打家劫舍I的基础上，将可偷房间连成环。

重点

  1. 将环展开，分情况讨论，以两种情况的最大值为结果
  2. 拆分数组的方法：
    • 最好理解的方法是遍历拆分，但是复杂度过高。
    • 所以干脆不拆分，以 start end 索引来截取想要的数组片段，缺点是边界条件容易出问题，人脑不好理解。

337-打家劫舍III

递归、二叉树和动态规划的结合（树形 DP）。

与前两个打家劫舍解题思路唯一的相关点：状态转移的思路不变，在偷与不偷中选择最佳情况。

重点

  1. dp 数组的定义：
    • 对于每个节点，dp[0]表示不偷，dp[1]表示偷，值分别为当前节点偷与不偷的最大数量。
    • 对于其他节点，栈来保存每一层递归的节点。
  2. 二叉树
    • 上层节点依赖于下层节点，所以是二叉树后序遍历递归方法。
      • 递归三部曲。
    • 状态转移公式在单层递归逻辑中。这道题递归就相当于遍历顺序了。

121-买卖股票的最佳时机

买卖股票的前两道题其实都可以用更好理解的贪心做出来，但是想要完全做出买卖股票这个系列，还是得用动态规划算法。

关键

  • dp 数组的含义，这个看视频就好。

    • 关键是理解“当天持有股票”是什么意思，与“当天买入股票”是两码事，易混淆。

  • 递推公式：

    • 概念。视频中概念描述得不太好理解，概念这么说会好理解些：

      • 持有股票的最大金额 == 为了持有股票所花费的最小金额，由于是花费，所以是负数。
      • 不持有股票的最大金额 == 卖出股票所赚得的最大金额。

    • 公式：

      • 实际推导一下图就很好理解了。

        输入：[7, 1, 5, 3, 6, 4]

        dp[i][0] dp[i][1]
        0 -7 0
        1 -1 0
        2 -1 4
        3 -1 4
        4 -1 5
        5 -1 5

122-买卖股票的最佳时机II

与 I 的唯一区别：

  • dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
  • I 只能买卖一次股票，所以这里花费的钱，只需为每张股票所需花费的价格即可。
  • II 能买卖多次股票，所以这里花费的钱，应该为 (之前赚的钱 - 买股票花费的钱)

对于这道题，其实我没透彻理解这个状态转移公式……

看不懂，放弃了，刷到后面看情况吧。

或许关键是看懂子问题？感觉自己陷入误区了，妄图去理解动态规划的全貌，导致脑袋爆栈。

[12.24] 五天后回头看这里的疑惑，发现状态转移公式还是很好理解的。

  • 今天持有股票所拥有的钱 = Math.max(前一天持有股票所拥有的钱, 前一天不持有股票 - 今天买股票所花费的钱);
  • 今天不持有股票所拥有的钱 = Math.max(前一天不持有股票所拥有的钱, 前一天持有股票所拥有的钱 + 今天卖股票所赚得的钱);

做算法果然不能钻牛角尖，适当放下，回头再看，思路就会清晰很多了。

123-买卖股票的最佳时机III

股票至多可买卖 2 次。

上一题的基础上多了几个状态。

188-买卖股票的最佳时机IV

股票至多可买卖 k 次。

需要将上一题抽象为可用变量表示的通式。

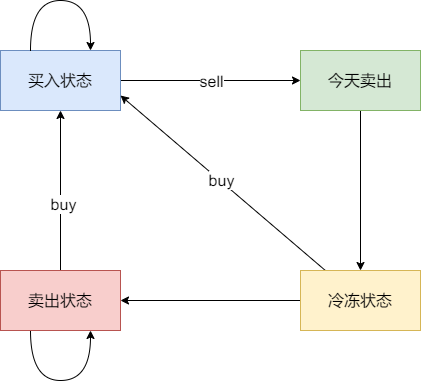
309-买卖股票的最佳时机含冷冻期

在 II 的基础上加上了冷冻期，较难。

重点

  • 定义 dp 数组
    • 未持有股票需划分为 3 种
      • 当前卖入股票状态。
      • 冷冻期状态。
      • 冷冻期后未持有股票状态。
  • 递推公式
    • 关键是搞清楚四种状态间的转移关系

714-买卖股票的最佳时机含手续费

在 II 的基础上加上了手续费，较简单。

只需在每次买卖股票时，状态转移公式中金额减去手续费即可。

子序列问题

300-最长递增子序列

定义 dp 数组：dp[i] 表示以 nums[i] 为结尾的最长递增子序列的长度。

重点：手动画图模拟感受一下过程。

10 9 2 5 3 7 101 18
1 1 1 2 2 3 4 4

分析

初始状态：当前的小范围内，最长子序列的长度为 1（①）

子问题：

  • 当范围 +1 时，需要将新加入进来的 nums[i] 逐个与先前范围内的 nums[j]（即前面最长公共子序列的最后一个也是最大的一个元素）作比较。（②）
  • 如果比最后一个元素还大，那么说明 dp[j]+1 可能是 dp[i] 的值。（②）
  • 逐个比较，dp[i] 的最终值为逐个比较后的最大值。（这步也是递推公式③的体现）

返回值为 dp 数组的最大值。（④）

代码与分析的对应

public int lengthOfLIS(int[] nums) {
    // 存储结果
    int result = 1;
    // 定义 dp 数组
    int len = nums.length;
    int[] dp = new int[len];
    // 1 初始化
    for (int i = 0; i < len; i++) {
        dp[i] = 1;
    }
    // 遍历
    for (int i = 1; i < len; i++) {
        for (int j = 0; j < i; j++) {
            // 2
            if (nums[i] > nums[j]) {
                // 3
                dp[i] = Math.max(dp[i], dp[j] + 1);
            }
        }
        // 4 返回值
        result = Math.max(result, dp[i]);
    }
    return result;
}

674-最长连续递增序列

与上一题的对比

  • 题意区别：
    • 上一题不要求连续
    • 本题要求连续。
  • 逻辑区别：
    • 上一题由于不要求连续，所以每当向后遍历一位数组后，都要再次遍历前面的数组。逐个对比，判断新值是否能够插入前面任意的一个最长序列。如果能则 +1，否则不变。
    • 本题由于要求连续，所以每当向后遍历一位数组后，只与当前位置的前一个元素做对比。
  • 代码区别：
    • 少了层 for 循环，还有递推公式的判断（对比元素的区别）。

718-最长重复子数组

关键

  • 定义 dp 数组：dp[i][j] 是以 i-1 与 j-1 元素作为结尾的公共子数组的长度。
  • 递推公式：
    • 如果 dp[i-1] != dp[j-1]，dp[i][j] = 0。
    • 如果 dp[i-1] == dp[j-1]，dp[i][j] = dp[i-1][j-1] + 1。
  • 初始化：定义 dp 数组时，以 i-1 与 j-1 作为结尾是为了避免初始化。
    • 如果 i,j=0，dp[i][j] 未定义，默认初始化为 0，dp[i][1] 与 dp[1][j] 按照 dp[i][0] 与 dp[0][j] 在递推公式中求出。
    • 如果 i,j=1，还需要遍历 dp[i][0] dp[0][j]，根据是否相等，判断初始化为 0 或 1，复杂度增加。
  • 遍历顺序：就是依次遍历二维数组。

1143-最长公共子序列

上一题要求公共序列元素连续，本题不要求连续。

区别

最大的区别在于递推公式：

  • if(text1.charAt(i - 1) == text2.charAt(j - 1))
    • dp[i][j] = dp[i - 1][j - 1] + 1;
  • if(text1.charAt(i - 1) == text2.charAt(j - 1))
    • dp[i][j] = Math.max(dp[i][j - 1], dp[i - 1][j]);
    • 解释：
      • 例如 abc 与 ace 做对比，c != e。
      • 所以对比 abc 与 ac 或 ab 与 ace，二者比较然后取最大值。

定义 dp 数组：dp[i][j] 是 nums1 范围 [0, i-1] 与 nums2 范围 [0, j-1] 公共子序列的长度。

返回值：根据 dp 数组定义，直接返回 dp[len1][len2] 即可。

1035-不相交的线

就是最长公共子序列问题，需要转换问题，看出本质。

53-最大子数组和

两种做法，贪心与动态规划。较简单。

392-判断子序和

编辑距离类入门题目。本题还可以用双指针解决，但是动态规划可以解决后续的编辑距离系列问题。

核心思路与最长公共子序列类似。

  • 定义 dp 数组

    • 二维 dp 数组表示的是两字符串每一个字符的对应情况。

    • 注意：由于初始状态可以由 0 在递归公式中自然推导出，所以 dp[i][j] 表示以 i-1 为结尾的 s 和以 j-1 为结尾的 t 的系统子序列长度，而不是 i 与 j。

  • 递推公式

    • 如果字符相同。
      • 长度 + 1。
    • 如果字符不同。
      • 长度不变。继续比较字符串 t 的下一个字符。

115-不同的子序列

（这道题的定义是区间，前一道题的定义是字符，还是有规律的吧，总结一下）

重点

  • 定义 dp 数组（代码随想录讲的听不懂，感觉评论区大佬的思路很清晰）
    • dp[i][j] 在 s[0] ~ s[i-1] 中，有多少个 t[0] ~ t[j-1] 的匹配

  • 递推公式（以 bag 与 bagg 举例，当遍历到第二个 g 时。）

    • 如果当前比较字符相等
      • s[0,i] 中 t[0,j] 的匹配数（bag） == s[0,i-1] 中 t[0,j-1] 的匹配数（ba） + s[0,i-1] 中 t[0,j] 的匹配数（除去当字符前后 bag 的匹配数）
    • 如果当前比较字符不相等
      • s[0,i] 中 t[0,j] 的匹配数 == s[0,i-1] 中 t[0,j] 的匹配数

  • 初始化 dp[i][0] 与 dp[0][j]

    • dp[i][0]：t 为空，s 中字符都删掉有一种空字符串的情况，初始化为 1。
    • dp[0][j]：s 为空，t 不为空，s 中有 0 种 t，初始化为 0。
    • dp[0][0]：s 为空，t 为空，1 种情况，初始化为 1。

联想

这道题的 dp 数组定义利用的是区间，前一道题的 dp 数组定义利用的是字符。

二者的区别？

  • 上一题判断是否出现，所以状态转移公式的理解较简单，只需逐个比较字符即可。
  • 本题要求出现了几次，较复杂，需要统计出具体个数，涉及一个区间内包含另一个区间个数的判断。

583-两个字符串的删除操作

与最长公共子序列类似，返回值处理一下即可。

72-编辑距离

关键在于递推公式，如何通过递推公式实现字符的增删改。

647-回文子串

定义 dp 数组：dp[i][j] 表示范围为 [i,j] 的子串是否是回文子串，boolean 类型。

516-最长回文子串

上一题要求连续，本题可以不连续。

定义 dp 数组：[i,j] 的回文子序列长度为 dp[i][j]

单调栈

739-每日温度

单调栈的使用场景就是，寻找当前元素左边或右边，第一个比当前元素大或者小的元素。

栈中的元素是递增或递减，该栈即为单调栈。

  • 递增：求当前元素左或右第一个比它大的元素
  • 递减：求当前元素左或右第一个比它小的元素

处理逻辑：

  • 遍历数组元素，按递增顺序放入栈中，如果不递增，则计算结果。

496-下一个更大元素I

503-下一个更大元素II

环形遍历数组，相比于复制数组然后拼接，取模法是更好的方法。

42-接雨水

本题按行方向统计，而非列方向。

84-柱状图中最大的矩形